Regression Kriging

Regression kriging (RK) mathematically equivalent to the universal kriging or kriging with external drift, where auxiliary predictors are used directly to solve the kriging weights. Regression kriging combines a regression model with simple kriging of the regression residuals. The experimental variogram of residuals is first computed and modeled, and then simple kriging (SK) is applied to the residuals to give the spatial prediction of the residuals.

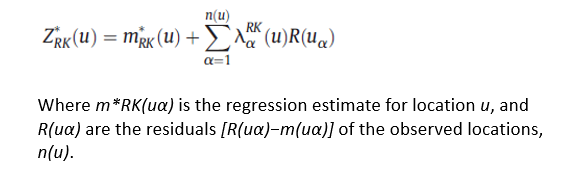
In this exerciser we will use following regression model for regression kriging of SOC:

• Generalized Linear Model

• Random Forest

• Meta Ensemble Machine Learning

We will use caret package for regression and gstat for geo-statistical modeling.

Load package

library(plyr)
library(dplyr)
library(gstat)
library(raster)
library(ggplot2)
library(car)
library(classInt)
library(RStoolbox)
library(caret)
library(caretEnsemble)
library(doParallel)
library(gridExtra)

Load Data

The soil organic carbon data (train and test data set) could be found here.

# Define data folder
dataFolder<-"D:\\Dropbox\\Spatial Data Analysis and Processing in R\\DATA_08\\DATA_08\\"

train<-read.csv(paste0(dataFolder,"train_data.csv"), header= TRUE) 
state<-shapefile(paste0(dataFolder,"GP_STATE.shp"))
grid<-read.csv(paste0(dataFolder, "GP_prediction_grid_data.csv"), header= TRUE) 

First, we will create a data.frame with SOC and continuous environmental data.

Power transformation

powerTransform(train$SOC)

## Estimated transformation parameter 
## train$SOC 
## 0.2523339

train$SOC.bc<-bcPower(train$SOC, 0.2523339)

Create dataframes

# train data
train.xy<-train[,c(1,24,8:9)]
train.df<-train[,c(1,24,11:21)]
# grid data
grid.xy<-grid[,c(1,2:3)]
grid.df<-grid[,c(4:14)]
#  define response & predictors
RESPONSE<-train.df$SOC.bc
train.x<-train.df[3:13]

Define coordinates

coordinates(train.xy) = ~x+y
coordinates(grid.xy) = ~x+y

Start foreach to parallelize for model fitting

mc <- makeCluster(detectCores())
registerDoParallel(mc)

Set control parameter

myControl <- trainControl(method="repeatedcv", 
                          number=10, 
                          repeats=5,
                          allowParallel = TRUE)

Generalized Linear Model

The Generalized Linear Model (GLM) is a flexible generalization of ordinary linear regression that allows for response variables that have error distribution models other than a normal distribution.

First will fit the GLM model with a comprehensive environmental co-variate, Then, we will compute and model the variogram of the of residuals of the GLM model and then simple kriging (SK) will be applied to the residuals to estimate the spatial prediction of the residuals (regional trend). Finally, GLM regression predicted results, and the SK kriged residuals will be added to estimate the interpolated soil organic C.

Fit Generalized Linear Model (GLM)

set.seed(1856)
GLM<-train(train.x,
           RESPONSE,
           method = "glm",
           trControl=myControl,
           preProc=c('center', 'scale'))
print(GLM)

## Generalized Linear Model 
## 
## 368 samples
##  11 predictor
## 
## Pre-processing: centered (11), scaled (11) 
## Resampling: Cross-Validated (10 fold, repeated 5 times) 
## Summary of sample sizes: 332, 331, 331, 331, 332, 331, ... 
## Resampling results:
## 
##   RMSE       Rsquared   MAE      
##   0.9423772  0.4742412  0.7310591

Variogram modeling of GLM residuals

First, we have to extract the residuals of RF model, we will use resid() function to get residuals of RF model

# Extract residuals
train.xy$residuals.glm<-resid(GLM)
# Variogram
v.glm<-variogram(residuals.glm~ 1, data = train.xy,cutoff=300000, width=300000/15)
# Intial parameter set by eye esitmation
m.glm<-vgm(0.15,"Exp",40000,0.05)
# least square fit
m.f.glm<-fit.variogram(v.glm, m.glm)
m.f.glm

##   model     psill    range
## 1   Nug 0.1085947     0.00
## 2   Exp 0.7943117 18818.22

#### Plot varigram and fitted model:
plot(v.glm, pl=F, 
     model=m.f.glm,
     col="black", 
     cex=0.9, 
     lwd=0.5,
     lty=1,
     pch=19,
     main="Variogram and Fitted Model\n Residuals of GLM model",
     xlab="Distance (m)",
     ylab="Semivariance")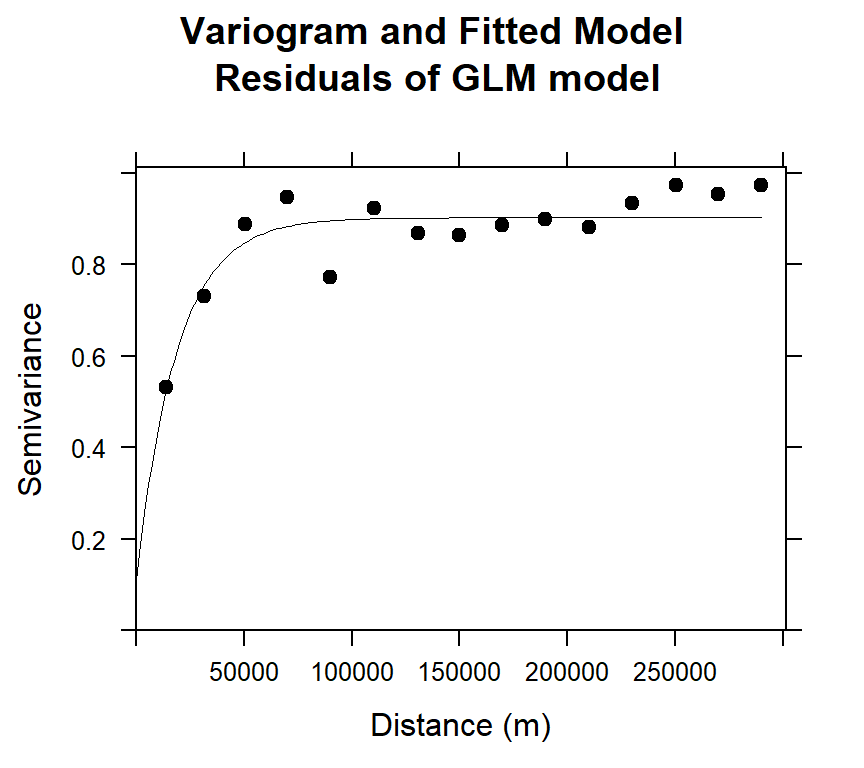

GLM Prediction at grid location

grid.xy$GLM <- predict(GLM, grid.df)

Simple Kriging Prediction of GLM residuals at grid location

SK.GLM<-krige(residuals.glm~ 1, 
              loc=train.xy,        # Data frame
              newdata=grid.xy,     # Prediction location
              model = m.f.glm,     # fitted varigram model
              beta = 0)            # residuals from a trend; expected value is 0     

## [using simple kriging]

Kriging prediction (SK + Regression Prediction)

grid.xy$SK.GLM<-SK.GLM$var1.pred
# Add RF predicted + SK preedicted residuals
grid.xy$RK.GLM.bc<-(grid.xy$GLM+grid.xy$SK.GLM)

Back transformation

We for back transformation we use transformation parameters

k1<-1/0.2523339                                   
grid.xy$RK.GLM <-((grid.xy$RK.GLM.bc *0.2523339+1)^k1)
summary(grid.xy)

## Object of class SpatialPointsDataFrame
## Coordinates:
##        min     max
## x -1245285  114715
## y  1003795 2533795
## Is projected: NA 
## proj4string : [NA]
## Number of points: 10674
## Data attributes:
##        ID             GLM              SK.GLM            RK.GLM.bc     
##  Min.   :    1   Min.   :-0.9197   Min.   :-2.663611   Min.   :-1.084  
##  1st Qu.: 2772   1st Qu.: 1.1693   1st Qu.:-0.104815   1st Qu.: 1.130  
##  Median : 5510   Median : 1.7494   Median : 0.008580   Median : 1.742  
##  Mean   : 5499   Mean   : 1.8277   Mean   : 0.001208   Mean   : 1.829  
##  3rd Qu.: 8237   3rd Qu.: 2.4885   3rd Qu.: 0.130163   3rd Qu.: 2.553  
##  Max.   :10999   Max.   : 4.2655   Max.   : 1.663093   Max.   : 4.995  
##      RK.GLM       
##  Min.   : 0.2819  
##  1st Qu.: 2.7028  
##  Median : 4.2374  
##  Mean   : 5.3003  
##  3rd Qu.: 7.1747  
##  Max.   :25.3268

Convert to raster

GLM<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "GLM")])
SK.GLM<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "SK.GLM")])
RK.GLM.bc<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "RK.GLM.bc")])
RK.GLM.SOC<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "RK.GLM")])

Plot predicted SOC

glm1<-ggR(GLM, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("GLM Predicted (BoxCox)")+
   theme(plot.title = element_text(hjust = 0.5))

glm2<-ggR(SK.GLM, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("SK GLM Residuals (BoxCox)")+
   theme(plot.title = element_text(hjust = 0.5))

glm3<-ggR(RK.GLM.bc, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("RK-GLM Predicted (BoxCox)")+
   theme(plot.title = element_text(hjust = 0.5))

glm4<-ggR(RK.GLM.SOC, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("RK-GLM Predicted (mg/g)")+
   theme(plot.title = element_text(hjust = 0.5))

grid.arrange(glm1,glm2,glm3,glm4, ncol = 4)  # Multiplot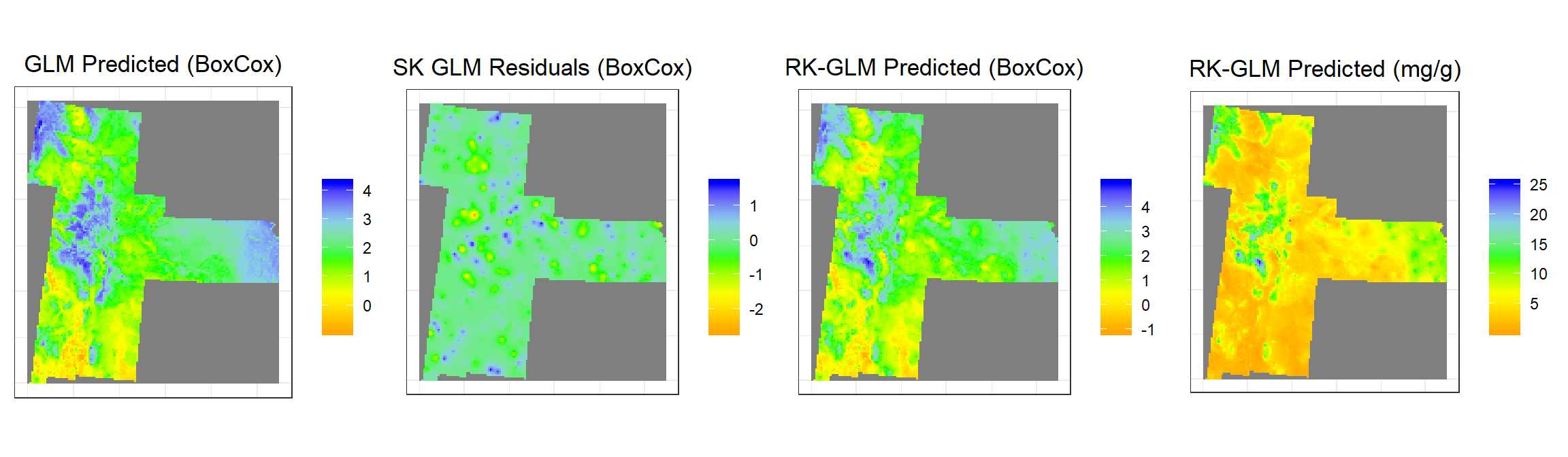 

Random Forest

Random forests, based on the assemblage of multiple iterations of decision trees, have become a major data analysis tool that performs well in comparison to single iteration classification and regression tree analysis [Heidema et al., 2006]. Each tree is made by bootstrapping of the original data set which allows for robust error estimation with the remaining test set, the so-called Out-Of-Bag (OOB) sample. The excluded OOB samples are predicted from the bootstrap samples and by combining the OOB predictions from all trees. The RF algorithm can outperform linear regression, and unlike linear regression, RF has no requirements considering the form of the probability density function of the target variable [Hengl et al., 2015; Kuhn and Johnson, 2013]. One major disadvantage of RF is that it is difficult to interpret the relationships between the response and predictor variables. However, RF allows estimation of the importance of variables as measured by the mean decrease in prediction accuracy before and after permuting OOB variables. The difference between the two are then averaged over all trees and normalized by the standard deviation of the differences (Ahmed et al., 2017).

First, will fit the RF model with a comprehensive environmental co-variate, Then, we will compute and model the variogram of the of residuals of the RF model and then simple kriging (SK) will be applied to the residuals to estimate the spatial prediction of the residuals (regional trend). Finally, RF regression predicted results, and the SK kriged residuals will be added to estimate the interpolated soil organic C.

Fit Random Forest Model (RF)

set.seed(1856)
mtry <- sqrt(ncol(train.x))             # number of variables randomly sampled as candidates at each split.
tunegrid.rf <- expand.grid(.mtry=mtry)
RF<-train(train.x,
           RESPONSE,
           method = "rf",
           trControl=myControl,
           tuneGrid=tunegrid.rf,
           ntree= 100,
           preProc=c('center', 'scale'))
print(RF)

## Random Forest 
## 
## 368 samples
##  11 predictor
## 
## Pre-processing: centered (11), scaled (11) 
## Resampling: Cross-Validated (10 fold, repeated 5 times) 
## Summary of sample sizes: 332, 331, 331, 331, 332, 331, ... 
## Resampling results:
## 
##   RMSE       Rsquared   MAE      
##   0.9345237  0.4780398  0.7210278
## 
## Tuning parameter 'mtry' was held constant at a value of 3.316625

Variogram modeling of RF residuals

First, we have to extract the residuals of RF model, we will use resid() function to get residuals of RF model

# Extract residials
train.xy$residuals.rf<-resid(RF)
# Variogram
v.rf<-variogram(residuals.rf~ 1, data = train.xy)
# Intial parameter set by eye esitmation
m.rf<-vgm(0.15,"Exp",40000,0.05)
# least square fit
m.f.rf<-fit.variogram(v.rf, m.rf)
m.f.rf

##   model     psill    range
## 1   Nug 0.0000000     0.00
## 2   Exp 0.1934731 15626.27

#### Plot varigram and fitted model:
plot(v.rf, pl=F, 
     model=m.f.rf,
     col="black", 
     cex=0.9, 
     lwd=0.5,
     lty=1,
     pch=19,
     main="Variogram and Fitted Model\n Residuals of RF model",
     xlab="Distance (m)",
     ylab="Semivariance")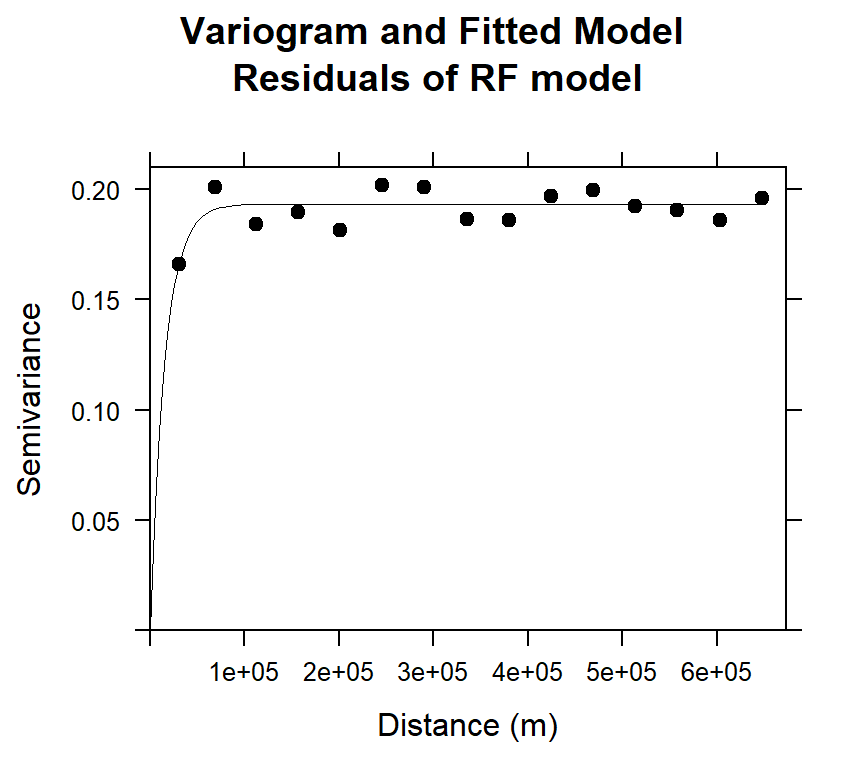

Prediction at grid location

grid.xy$RF <- predict(RF, grid.df)

Simple Kriging Prediction of RF residuals at grid location

SK.RF<-krige(residuals.rf~ 1, 
              loc=train.xy,        # Data frame
              newdata=grid.xy,     # Prediction location
              model = m.f.rf,      # fitted varigram model
              beta = 0)            # residuals from a trend; expected value is 0     

## [using simple kriging]

Kriging prediction (SK+Regression)

grid.xy$SK.RF<-SK.RF$var1.pred
# Add RF predicted + SK preedicted residuals
grid.xy$RK.RF.bc<-(grid.xy$RF+grid.xy$SK.RF)

Back transformation

We for back transformation we use transformation parameters

k1<-1/0.2523339                                   
grid.xy$RK.RF <-((grid.xy$RK.RF.bc *0.2523339+1)^k1)
summary(grid.xy)

## Object of class SpatialPointsDataFrame
## Coordinates:
##        min     max
## x -1245285  114715
## y  1003795 2533795
## Is projected: NA 
## proj4string : [NA]
## Number of points: 10674
## Data attributes:
##        ID             GLM              SK.GLM            RK.GLM.bc     
##  Min.   :    1   Min.   :-0.9197   Min.   :-2.663611   Min.   :-1.084  
##  1st Qu.: 2772   1st Qu.: 1.1693   1st Qu.:-0.104815   1st Qu.: 1.130  
##  Median : 5510   Median : 1.7494   Median : 0.008580   Median : 1.742  
##  Mean   : 5499   Mean   : 1.8277   Mean   : 0.001208   Mean   : 1.829  
##  3rd Qu.: 8237   3rd Qu.: 2.4885   3rd Qu.: 0.130163   3rd Qu.: 2.553  
##  Max.   :10999   Max.   : 4.2655   Max.   : 1.663093   Max.   : 4.995  
##      RK.GLM              RF              SK.RF           
##  Min.   : 0.2819   Min.   :-0.2965   Min.   :-1.0396339  
##  1st Qu.: 2.7028   1st Qu.: 1.1496   1st Qu.:-0.0487090  
##  Median : 4.2374   Median : 1.8344   Median :-0.0008605  
##  Mean   : 5.3003   Mean   : 1.8425   Mean   :-0.0063920  
##  3rd Qu.: 7.1747   3rd Qu.: 2.5434   3rd Qu.: 0.0401477  
##  Max.   :25.3268   Max.   : 4.6236   Max.   : 1.0526308  
##     RK.RF.bc           RK.RF        
##  Min.   :-0.8629   Min.   : 0.3779  
##  1st Qu.: 1.1342   1st Qu.: 2.7114  
##  Median : 1.8129   Median : 4.4496  
##  Mean   : 1.8361   Mean   : 5.2190  
##  3rd Qu.: 2.5500   3rd Qu.: 7.1623  
##  Max.   : 5.2743   Max.   :28.6076

Convert to raster

RF<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "RF")])
SK.RF<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "SK.RF")])
RK.RF.bc<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "RK.RF.bc")])
RK.RF.SOC<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "RK.RF")])

Plot predicted SOC

rf1<-ggR(RF, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("RF Predicted (BoxCox)")+
   theme(plot.title = element_text(hjust = 0.5))

rf2<-ggR(SK.RF, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("SK RF Residuals (BoxCox)")+
   theme(plot.title = element_text(hjust = 0.5))

rf3<-ggR(RK.RF.bc, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("RK-RF Predicted (BoxCox)")+
   theme(plot.title = element_text(hjust = 0.5))

rf4<-ggR(RK.RF.SOC, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("RK-RF Predicted (mg/g)")+
   theme(plot.title = element_text(hjust = 0.5))

grid.arrange(rf1,rf2,rf3,rf4, ncol = 4)  # Multiplot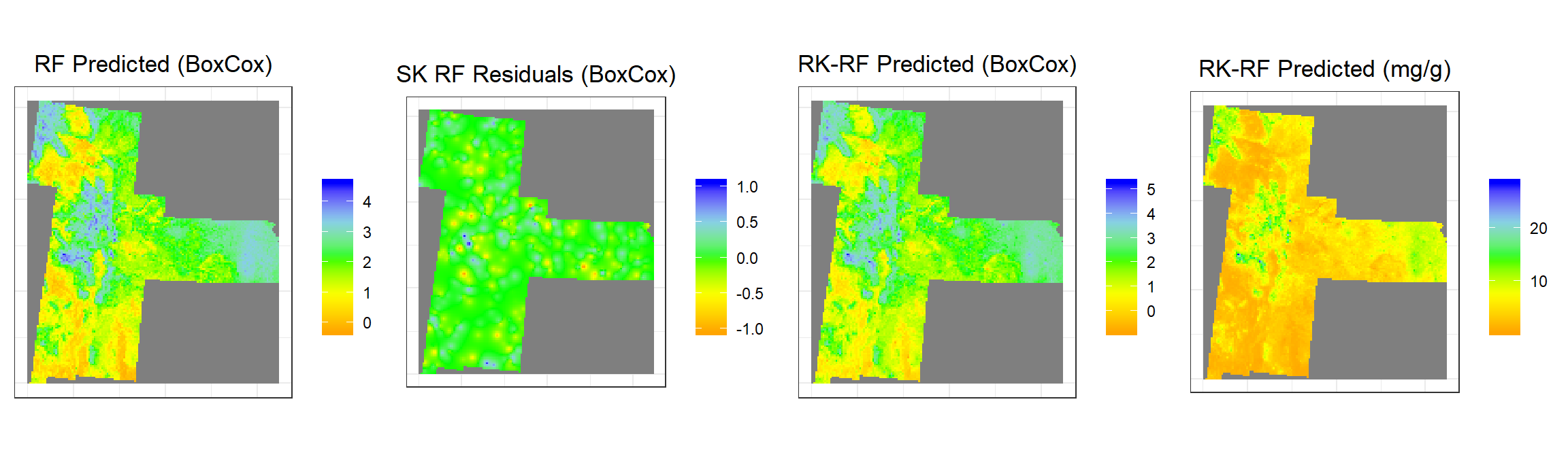 

Meta Ensemble Machine Learning

Ensemble machine learning methods use multiple learning algorithms to obtain better predictive performance than could be obtained from any of the constituent learning algorithms. Many of the popular modern machine learning algorithms are ensembles. For example, Random Forest and Gradient Boosting Machine are both ensemble learners. However, stacked generalization or stacking or Supper Learning (Wolpert, 1992) that introduces the concept of a meta learner that ensemble or combined several strong, diverse sets of machine learning models together to get better prediction. In this modeling approach, each base level models are trained first, then the meta-model is trained on the outputs of the base level models. The base level models often consist of different learning algorithms and therefore stacking ensembles are often heterogeneous.

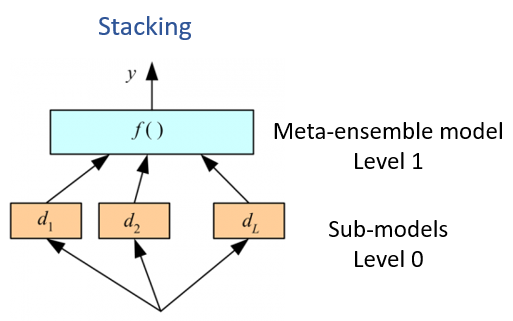
We will built a random forest (RF) regression model by stacking of GLM and RF regression models (sub-models) to predict SOC.

Create a model list

algorithmList <- c("glm","rf")

Fit all models

We will use caretList() function of caretEnsemble package to fit all models

set.seed(1856)
models<-caretList(train.x, RESPONSE,
                  methodList=algorithmList,
                  trControl=myControl,
                  preProc=c('center', 'scale')) 

Performance of sub-models

results.all <- resamples(models)
cv.models<-as.data.frame(results.all[2])
summary(results.all)

## 
## Call:
## summary.resamples(object = results.all)
## 
## Models: glm, rf 
## Number of resamples: 50 
## 
## MAE 
##          Min.   1st Qu.    Median      Mean   3rd Qu.     Max. NA's
## glm 0.5299362 0.6759200 0.7317607 0.7323044 0.7936931 1.049905    0
## rf  0.5559114 0.6511738 0.7138410 0.7195130 0.7839459 1.010871    0
## 
## RMSE 
##          Min.   1st Qu.    Median      Mean  3rd Qu.     Max. NA's
## glm 0.6654767 0.8742916 0.9524959 0.9435913 1.034049 1.308432    0
## rf  0.6854099 0.8645415 0.9399393 0.9306508 1.010455 1.261128    0
## 
## Rsquared 
##          Min.   1st Qu.    Median      Mean   3rd Qu.      Max. NA's
## glm 0.1626709 0.4161093 0.4726874 0.4767778 0.5456160 0.6850497    0
## rf  0.2138578 0.4080458 0.4848379 0.4868120 0.5505441 0.7026729    0

Plot K-fold Cross Validation results (MAE, RMSE, R2)

dotplot(results.all, 
        scales =list(x = list(relation = "free")),
        panelRange =T,  conf.level = 0.9, 
        between = list(x = 2))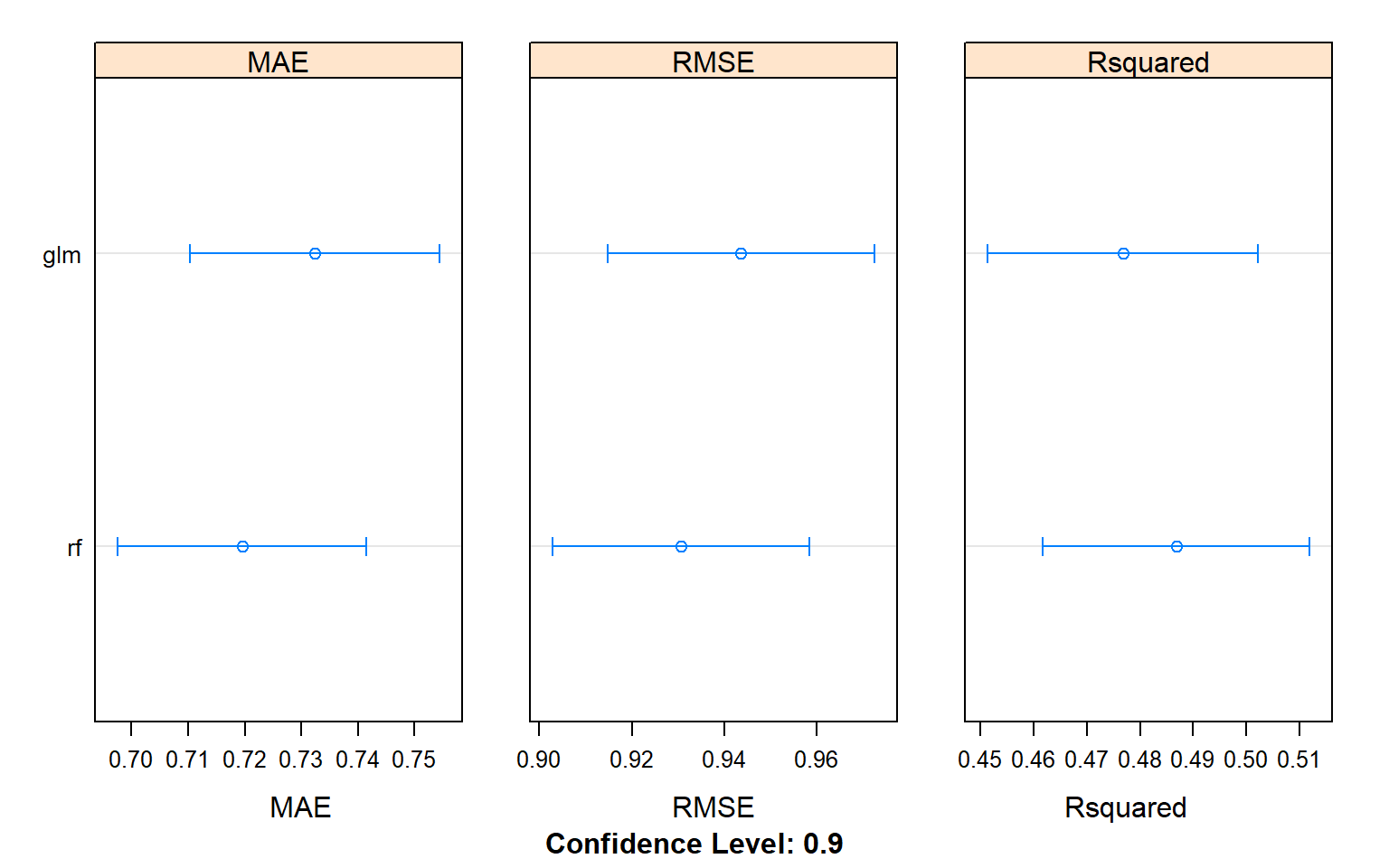

Combine several predictive models via stacking

We will use caretStack() function with “method” parameter “rf” for random forest regression model

stackControl <- trainControl(method="repeatedcv", 
                             number=10, 
                             repeats=5, 
                             savePredictions=TRUE)
set.seed(1856)
stack.rf <- caretStack(models, 
                       method="rf",
                       trControl=stackControl)

## note: only 1 unique complexity parameters in default grid. Truncating the grid to 1 .

Ensemble results

stack.rf.cv<-stack.rf$ens_model$resample
stack.rf.results<-print(stack.rf)

## A rf ensemble of 2 base models: glm, rf
## 
## Ensemble results:
## Random Forest 
## 
## 1840 samples
##    2 predictor
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 5 times) 
## Summary of sample sizes: 1656, 1656, 1656, 1656, 1656, 1656, ... 
## Resampling results:
## 
##   RMSE       Rsquared   MAE      
##   0.8861827  0.5296594  0.6690021
## 
## Tuning parameter 'mtry' was held constant at a value of 2

Variogram modeling of residuals

Now, we will calculate residuals of RF model since resid() function does not work here.

train.xy$REG.SOC.bc<-predict(stack.rf,train.x)
train.xy$residuals.stack<-(train.xy$SOC.bc-train.xy$REG.SOC.bc)

# Variogram
v.stack<-variogram(residuals.stack~ 1, data = train.xy)
# Intial parameter set by eye esitmation
m.stack<-vgm(0.15,"Exp",40000,0.05)
# least square fit
m.f.stack<-fit.variogram(v.stack, m.stack)
m.f.stack

##   model      psill    range
## 1   Nug 0.74019315      0.0
## 2   Exp 0.02392722 196106.8

#### Plot varigram and fitted model:
plot(v.stack, pl=F, 
     model=m.f.stack,
     col="black", 
     cex=0.9, 
     lwd=0.5,
     lty=1,
     pch=19,
     main="Variogram and Fitted Model\n Residuals of meta-Ensemble model",
     xlab="Distance (m)",
     ylab="Semivariance")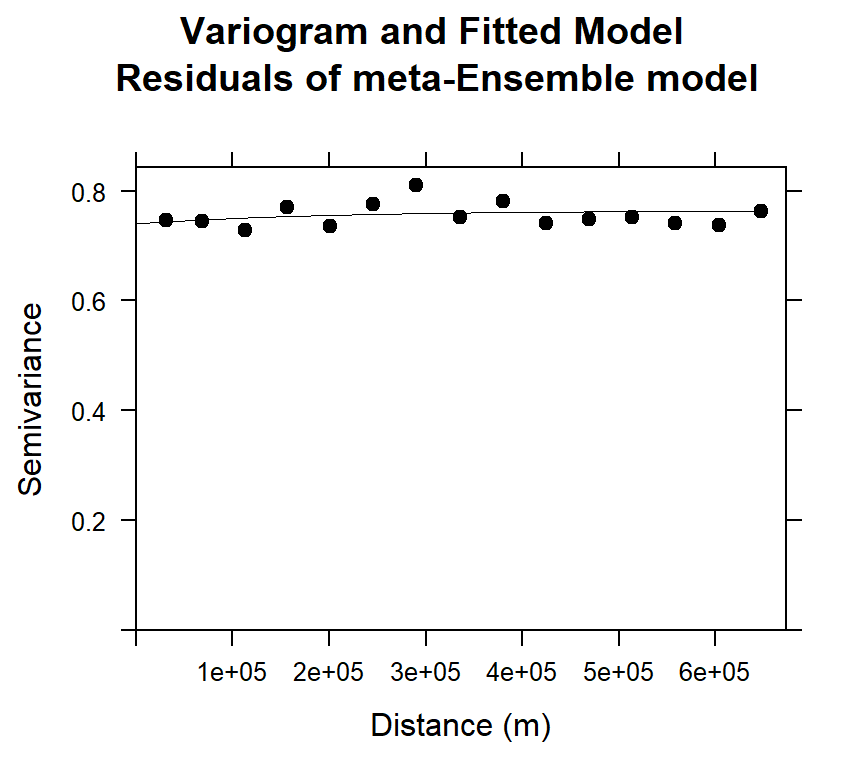

Prediction at grid location

grid.xy$stack <- predict(stack.rf, grid.df)

Simple Kriging Prediction of RF residuals at grid location

SK.stack<-krige(residuals.stack~ 1, 
              loc=train.xy,        # Data frame
              newdata=grid.xy,     # Prediction location
              model = m.f.stack,    # fitted varigram model
              beta = 0)            # residuals from a trend; expected value is 0     

## [using simple kriging]

Kriging prediction (SK+Regression)

grid.xy$SK.stack<-SK.stack$var1.pred
# Add RF predicted + SK preedicted residuals
grid.xy$RK.stack.bc<-(grid.xy$stack+grid.xy$SK.stack)

Back transformation

We for back transformation we use transformation parameters

k1<-1/0.2523339                                   
grid.xy$RK.stack <-((grid.xy$RK.stack.bc *0.2523339+1)^k1)
summary(grid.xy)

## Object of class SpatialPointsDataFrame
## Coordinates:
##        min     max
## x -1245285  114715
## y  1003795 2533795
## Is projected: NA 
## proj4string : [NA]
## Number of points: 10674
## Data attributes:
##        ID             GLM              SK.GLM            RK.GLM.bc     
##  Min.   :    1   Min.   :-0.9197   Min.   :-2.663611   Min.   :-1.084  
##  1st Qu.: 2772   1st Qu.: 1.1693   1st Qu.:-0.104815   1st Qu.: 1.130  
##  Median : 5510   Median : 1.7494   Median : 0.008580   Median : 1.742  
##  Mean   : 5499   Mean   : 1.8277   Mean   : 0.001208   Mean   : 1.829  
##  3rd Qu.: 8237   3rd Qu.: 2.4885   3rd Qu.: 0.130163   3rd Qu.: 2.553  
##  Max.   :10999   Max.   : 4.2655   Max.   : 1.663093   Max.   : 4.995  
##      RK.GLM              RF              SK.RF           
##  Min.   : 0.2819   Min.   :-0.2965   Min.   :-1.0396339  
##  1st Qu.: 2.7028   1st Qu.: 1.1496   1st Qu.:-0.0487090  
##  Median : 4.2374   Median : 1.8344   Median :-0.0008605  
##  Mean   : 5.3003   Mean   : 1.8425   Mean   :-0.0063920  
##  3rd Qu.: 7.1747   3rd Qu.: 2.5434   3rd Qu.: 0.0401477  
##  Max.   :25.3268   Max.   : 4.6236   Max.   : 1.0526308  
##     RK.RF.bc           RK.RF             stack           SK.stack       
##  Min.   :-0.8629   Min.   : 0.3779   Min.   :-1.218   Min.   :-0.21691  
##  1st Qu.: 1.1342   1st Qu.: 2.7114   1st Qu.: 1.126   1st Qu.:-0.05766  
##  Median : 1.8129   Median : 4.4496   Median : 1.826   Median :-0.02026  
##  Mean   : 1.8361   Mean   : 5.2190   Mean   : 1.840   Mean   :-0.01805  
##  3rd Qu.: 2.5500   3rd Qu.: 7.1623   3rd Qu.: 2.578   3rd Qu.: 0.01338  
##  Max.   : 5.2743   Max.   :28.6076   Max.   : 5.223   Max.   : 0.17909  
##   RK.stack.bc        RK.stack      
##  Min.   :-1.257   Min.   : 0.2205  
##  1st Qu.: 1.117   1st Qu.: 2.6744  
##  Median : 1.804   Median : 4.4215  
##  Mean   : 1.822   Mean   : 5.3440  
##  3rd Qu.: 2.552   3rd Qu.: 7.1725  
##  Max.   : 5.202   Max.   :27.7264

Convert to raster

stack<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "stack")])
SK.stack<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "SK.stack")])
RK.stack.bc<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "RK.stack.bc")])
RK.stack.SOC<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "RK.stack")])

Plot predicted SOC

s1<-ggR(stack, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("Meta-Ensemble Predicted (BoxCox)")+
   theme(plot.title = element_text(hjust = 0.5))

s2<-ggR(SK.stack, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("SK Meta-Ensemble Residuals (BoxCox)")+
   theme(plot.title = element_text(hjust = 0.5))

s3<-ggR(RK.stack.bc, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("RK-Meta-Ensemble Predicted (BoxCox)")+
   theme(plot.title = element_text(hjust = 0.5))

s4<-ggR(RK.stack.SOC, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("RK-Meta-Ensemble Predicted (mg/g)")+
   theme(plot.title = element_text(hjust = 0.5))

grid.arrange(s1,s2,s3,s4, ncol = 4)  # Multiplot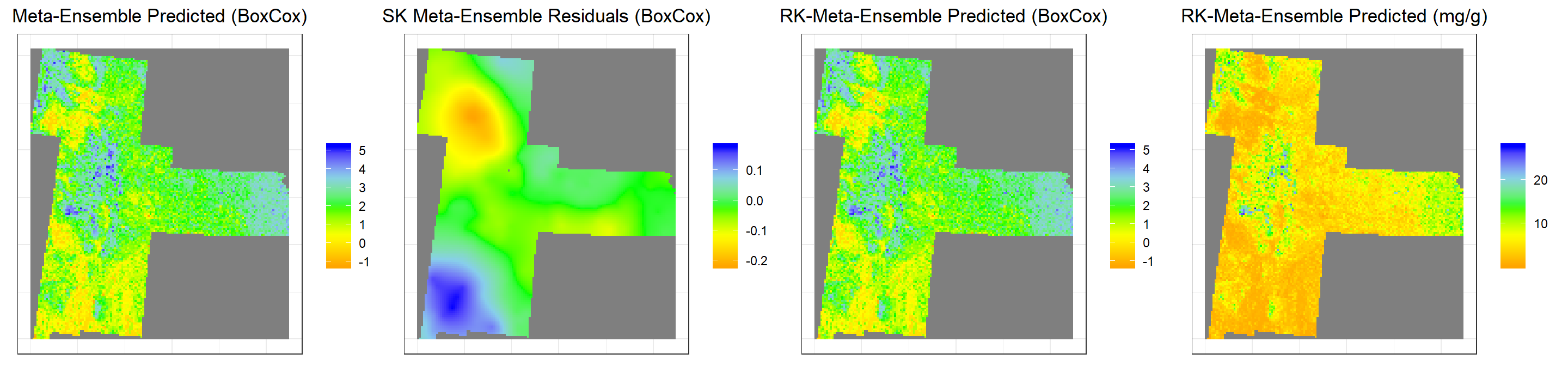 

rm(list = ls())