
Geostatistical Interpolation
Spatial interpolation using geostatistical techniques has been widely used to map environmental variables. Geostatistics relies on on the concept of random function, whereby the set of unknown values is considered as a set of spatially dependent random variables. The random function concepts allows to account for structures in the spatial variation of the attributes. Unlike the deterministic interpolation approaches, geostatistics assumes that all values in a domain are the result of a random process with dependence. At any particular location, the uncertainty of attribute value is estimated from a set of possible outcomes of the random variable at that location. This way we can model the uncertainty of spatial prediction over the entire study area.
The main steps involved in geostatistical interpolation model are:
Examining the data (distribution, trends, directional components, outliers)
Calculating the empirical semivariogram or covariance values
Fitting a model to the empirical values.
Generating the matrices of kriging equations.
Solving them to obtain a predicted value and the error (uncertainty) associated with it for each location in the output surface.
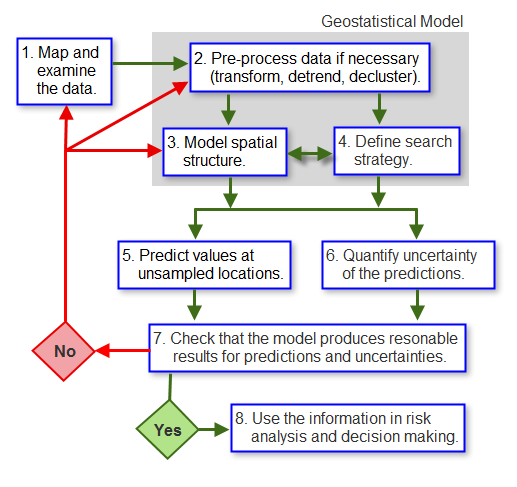
Work Flow Geostatistical Interpolation (Source: http://pro.arcgis.com/en/pro-app/help/analysis/geostatistical-analyst/the-geostatistical-workflow.htm )
Geostatistics is widely used in many areas of science and engineering, for example:
To quantify mineral resources in mining industry
Pollution mapping and risk assessment in the environmental sciences
Digital mapping of soil variables
Prediction of temperatures, rainfall, and associated variables (such as acid rain) in meteorological applications
In the area of public health
We will cover following area in Geostatistical Interpolation section:
-
-
Generalized Linear Model
Random Forest
Meta-Ensemble Machine Learning